II. REGRESSION: R functions for multiple regression and its ramifications
(a) Topic 1: Basics [Chapter 3 in Jank] Simple and multiple regression
In this section we will look at sales/advertising/income data and consider simple and multiple linear regression models.
a.1 Sales vs. advertising
 vs.
vs. 
Here is (was) a cool animation for finding the regression line: Animation for regression. [Sorry, this stopped working after I installed the new version of Java. No idea why this is happening with Java.]
Here is a graphical explanation of what linear regression does. Note the meaning of SST, SSE and SSR from which we obtain R^2 = SSR/SST which is always between 0 and 1. (Could SST, SSE and SSR be interpreted as Total Cholesterol, Bad Cholesterol and Good Cholesterol, resp.?)
Example: (Sales vs. Advertising) Let's use the sales and advertising data [Table3.1Sales-Advertising.csv] and analyze it.
-
- How did Rcmdr find the green line on the graph? This is the regression line, and here is what we do to find it. (To find the regression equation, you will need to use Rcmdr's Statistics >
Fit Models > Linear Regression.) So, the regression line is Sales = 51.489 + 7.527 x Advertising with R-squared = 0.24. What do these numbers mean?
- The intercept 51.489 is how much we might expect to make if there is no advertising, i.e., Advertising = 0. (But be careful about this! Why?)
- The coefficient 7.527 means that for each unit increase in Advertising expenditure, we expect to have an additional sales of 7.527.
- It is very important to look at the Pr(> | t |) values to get a feel for how significant is a coefficient. (This is the p-value we introduced in the Coke-Pepsi hypothesis testing experiment. Here, we have H0: The coefficient of a variable = 0.)
- You can consider the ratio of "Estimate to Std. Error" (which gives the t value) as a Signal-to-Noise ratio. If this ratio is high [and the Pr(> | t |) is low] then the coefficient is non-zero and so the result is significant. The values indicated by *, **, etc., indicate the significance codes (smaller code, the more significant is the coefficient.)
>>Predictions
How do we predict the sales for given advertising levels and also find prediction and confidence intervals?
- The next two commands are used to do the predictions:
newPoint <- data.frame(ADVT=10.25); newPoint
predict(RegModel.1,newPoint,interval="prediction")
- With the help of Rcmdr, we get these results. (The highlighted commands are entered manually in the Rcmdr window. The package UsingR and its function simple.lm is optional.) Note that with a single R line we can easily obtain the prediction results.
- Good news! Basically, the only time you will need to enter commands in Rcmdr is when you are doing predictions. We will do this one more time with multiple regression below. We will also look at a nice correlation plot (corrplot) package where you will enter a few simple commands. All other commands are generated by Rcmdr automatically.
Here are a few more examples of predictions. The inputs and results should be clear from the context.
newPoints <- data.frame(ADVT=c(8:11))
newPoints
ADVT
1 8
2 9
3 10
4 11
predict(RegModel.1,newPoints,interval="prediction")
fit lwr upr
1 112.0672 79.10412 145.0304
2 119.5945 88.28846 150.9005
3 127.1217 96.49693 157.7466
4 134.6490 103.66509 165.6329
You could also enter
data.frame(ADVT=c(8,9.2,10.7))
to predict for 8, 9.2 and 10.7.
This is also possible:
data.frame(ADVT=c(seq(8,10.5,by=0.5)))
if you want to predict for 8, 8.5, 9, 9.5, 10, 10.5.
¶
Once the regression model is computed, we need to check certain things. Perhaps most importantly, the errors must be approximately normally distributed. This can be done graphically as follows:
- Models > Graphs > Basic diagnostic plots: The top two tell us how errors look.
- Models > Graphs > Residual quantile comparison plot: If the dots are all approximately on or near the line, then the normality of the errors is assured.
Example : (Anscombe's Quartet) Here's an amazing example of four problems with very different datasets which give the same results. Anscombe's quartet.
¶
Example : (Your Data) Your height-handspan data [Height-Gender-Handspan-2017.csv]. We will see if this model works well to estimate someone'e height from his/her handspan.
New <- data.frame(Handspan=xx)
predict(RegModel.1,New,interval="prediction")
¶
Exercise: Consider this house price dataset [HousePrices-Data.csv] for 124 houses. Do a simple regression with Price as dependent variable and SqrFt as independent variable. Perform analysis similar to what we did above with the advertising/sales problem. (Answer: Regression equation is Price = 259.88 + 120.16 x SqrFt.)
a.2 Sales vs. advertising and income
 vs.
vs.  and
and 
Example: (Sales vs. Advertising and Income) Now we use the sales vs. advertising and income data [Table 3.1 Sales-Advertising-Income.csv]. So, this is a multiple regression problem which is solved as follows:
- Rcmdr can plot the 3D graph of the dataset and even show the fitted linear surface. It also finds the coefficients of the regression equation. The results are here without the 3D graph. (To find the regression equation, you will need to use Rcmdr's Statistics >
Fit Models > Linear Regression.) The regression equation is then Sales = 36.894 + 5.069 x Advertising + 0.808 x Income with R-squared = 0.45.
- The comments made about the significance of the coefficients also apply here.
>>Predictions
We should be able to predict the Sales from the given values of Advertising and Income as follows:
new <- data.frame(ADVT=8, INCOME=53)
new
predict(RegModel.1, new, interval="prediction")
- This is quite easy with R and the results are found here. (Note again that the highlighted commands are entered manually in the Rcmdr window.) The confint() command used here gives the 95% confidence intervals for the regression coefficients.
¶
Exercise: Consider the same house price dataset [HousePrices-Data.csv] for 124 houses used above. Now use SqrFt, LotSize, Bedrooms and Bathrooms as independent variables and Price as dependent variable and perform a multiple regression.
a.3 Customers' Spending Patterns (Direct Marketing)
Example: (Direct Marketing) Let's retun to the same dataset we looked at the first day, i.e., the direct marketing data. Recall that this dataset has four numerical variables and the rest are qualitative. Let's do a multiple regression on these four varibles with AmountSpent as the dependent variable. Here's the Direct marketing data
set [Table 2.6 DirectMarketing.csv] again.
- The model now is: RegModel.1 <- lm(AmountSpent~Catalogs+Children+Salary, data=Dataset)
- The regression equation is found as AmountSpent = -442 + .02 x Salary + 47.7 x Catalogs - 198 x Children
- We also have R^2 = .6584 which is reasonably high.
- The following command gives the 95% CI for all coefficients. Interpretation?
- > confint(RegModel.1)
2.5 % 97.5 %
(Intercept) -548.17071899 -337.3451739
Catalogs 42.28849708 53.1021521
Children -232.22618388 -165.1631964
Salary 0.01924234 0.0215693
- Intercept is always the value of the response variable when everything else is set at zero. But in this case the negative intercept (-442) really has no meaning.
We can also do a
correlation plot of the above dataset using corrplot. Rcmdr
first generates the correlation matrix which we call M and then ask corrplot to
do the work. Here are the results. You can
use the following commands after creating the M matrix of correlations:
corrplot(M, method = "ellipse")
or
corrplot(M, order = "FPC",method="ellipse")
¶
Example : (BIG Stuff!) How long would it take to generate 1,000,000 observations (standard normal) for 100 variables plus the means? Once that is done, how long does it take to run a 100 independent variable multiple regression problem with the 1,000,000 observations? (Just a minute or two!) We will do this in class.
¶
Exercise: The problem statement for this Education Level/Gender/Income problem is here. You will need this Excel data file [Education-Gender-Income.xlsx] to import into Rcmdr and do the calculations.
a.4 House Prices (Will be covered)

Example: (House Prices) This is a more challenging problem with qualitative factors (such as Yes/No, North/West/East) for some variables in the dataset [Table2.1HousePrices.csv]. To find the regression equation, you will need to use Rcmdr's Statistics > Fit Models > Linear Model as LinearModel.1 <- lm(Price ~ Bathrooms + Bedrooms + Brick + Neighborhood + Offers + SqFt, data=Dataset). The confint(LinearModel.1) command will produce the confidence intervals for coefficients. Here are the results.
Please note; important!: The output indicates that Brick[T.Yes] coefficient is 17297.350. This means that as you move from the base level of Brick[T.No] to Brick[T.Yes], you would expect an increase of about 17297.35 in the sale price of your house. (The factor name that doesn't appear in the list is the base level.) Similarly, the base level for Neighborhood is Neighborhood[T.East] which doesn't appear in the list. So, 1560.579 for Neighborhood[T.North] is how much is the expected difference between the price of a house in the East vs. in the North.
Prediction of the dependent variable when factors are present (such as Brick, Neighboorhood) can be a little tricky. Here is what you need to do if you want to predict the price of a house with 3 bathrooms, 5 bedrooms, brick, north neighborhood, 2 offers and 2000 sqft. As usual, the highlighted commands are entered manually as follows:
new <- data.frame(Bathrooms=3, Bedrooms=5, Brick="Yes", Neighborhood="North",
Offers=2, SqFt=2000)
predict(LinearModel.1,new,interval="prediction")
I used the corrplot package to plot the correlations between different numerical variables in this example. Here is the result.
¶
Top of page
(b) Topic 2: Making models more flexible [Chapter 4 in Jank] Dummy variables, interaction terms, data transformations, nonlinear regression models
b.1 "Dummy" variables [EXCLUDED!]
Example (very simple): (Trucking) Suppose we have this dataset [Trucking-Factor.csv] where we want to estimate the travel time, given, (i) distance travelled, (ii) number of deliveries and (iii) truck type. Note that truck type (Pickup, or Van) is not given as a numerical value. In previous regression examples, the variables were all numerical, but now the truck type is a categorical variable. So, what do we do now?
- We can introduce a dummy (indicator) variable and indicate, say, Pickup by 0 and Van by 1. (So, Pickup is the base here.) This gives us the new (re-coded) dataset [Trucking-Dummy.csv]. Now, we can solve the problem the usual way and find Time = 0.5222 + 0.0464 x Km + 0.7102 x Deliveries + 0.9 x TruckType. (Here, if we decide to use a Van rather than a Pickup, our expected travel time goes up by 0.9 hours.)
- What if we had three types of vehicles? Pickup, Van and Scooters (for small deliveries)? Now we would have to consider a more complex set of dummy variables. (I will show in class.)
- But there is an easier way to do these things. Use the original dataset [Trucking-Factor.csv]. Rcmdr will recognize that TruckType is a factor and will let you use the Linear Model option.
- The result now will be Time = 0.5222 + 0.0464 x Km + 0.7102 x Deliveries + 0.9 x TruckType[T.Van]. Once again, if we move from the base Pickup to Van, the coefficient 0.9 of TruckType[T.Van] tells us that we spend about 0.9 hours longer on the road.
>>Predictions
New <- data.frame(Km=45, Deliveries=3, TruckType="Van")
predict(LinearModel.1, New, interval="prediction")
¶

Example: (Discrimination?) Let's consider the dataset for salaries [Table4.1GenderDiscrimination-Factor.csv]. When we ignore the gender and plot the dataset, we are missing out on the information inherent in the gender differences. Only when we plot the data according to gender group, we see a more clear picture. The Rcmdr results are here. So, if we just consider the Experience and Salary columns, the regression equation is found as Salary = 59033.1 + 1727.3 x Experience. (R-squared = 0.31.) But is this accurate?¶
But the workers' gender may make a difference in the salary. To account for this just use the "Linear model". Rcmdr knows that Gender is a factor. If you pick it as an independent variable, R figures out the rest and you get the result as Salary = 53260 + 1744 x Experience + 17020 x Gender[T.Male]. (You can do this as an exercise!)
So, here is the summary of what we have found so far:
- Starting salary for females is 53,260.
- Starting salary for males is 53,260 + 17,020 = 70,280. (Discrimination?)
- Each additional year of experience is worth 1,744 for either gender. (Seems strange! We will fix this soon with an interaction term.)
- The Rcmdr results of this analysis.
¶
b.2 Interaction terms [EXCLUDED!]
This is a somewhat difficult material. So, let me give you a few real-life examples of interaction (from Wikipedia.)


-
Interaction between smoking and inhaling
asbestos fibres: Both raise lung carcinoma risk, but exposure to asbestos
multiplies the cancer risk in smokers and non-smokers. Here, the
joint effect of inhaling asbestos and smoking is higher than the sum of both effects.
Now, back to our discussion...
-
- Background material for interaction on Wikipedia.
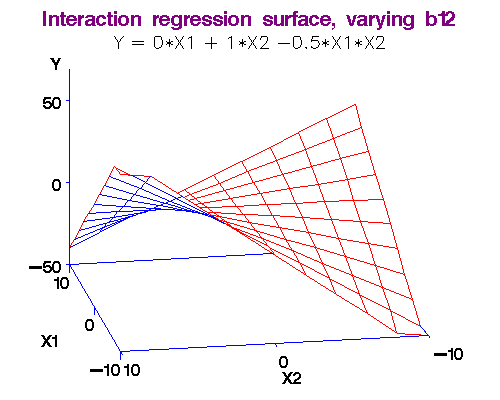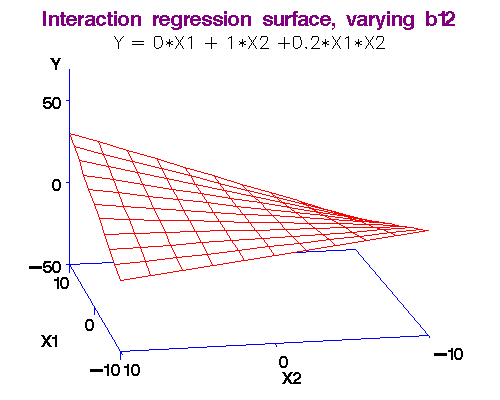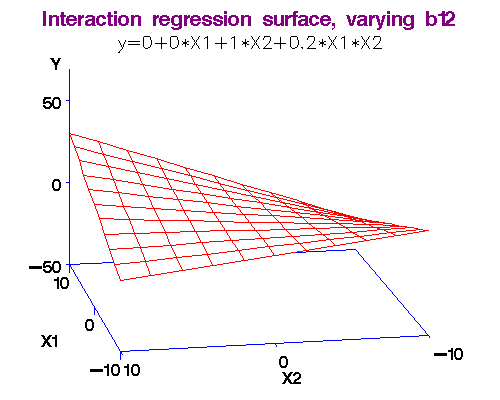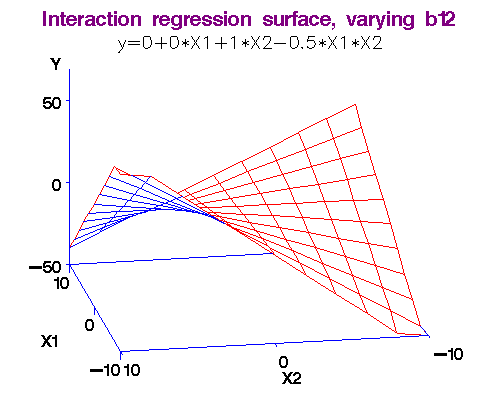
Example: (More Discrimination?)We noted above that each additional year of experience is 1,744 for either gender. But this is not quite logical. Could it be more for males? Or, for females? We analyse this using an interaction term in the form Experience*Gender in the Linear Model. That is, just use the "Linear model" and incorporate the product of Experience and Gender new "variable." Rcmdr figures out what to do and finds the result. Here again is the dataset for salaries [Table4.1GenderDiscrimination-Factor.csv] and the model is,
LinearModel.1 <- lm(Salary ~ Experience + Gender + Experience*Gender,
data=Dataset).
The output is obtained as follows. (The coefficients are shown in bold font, and Experience:Gender[T.Male]
is the interaction term.)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 66333.6 2811.7 23.592 < 2e-16 ***
Experience 666.7 206.5 3.228 0.00145 **
Gender[T.Male] -8034.3 4110.6 -1.955 0.05201 .
Experience:Gender[T.Male] 2086.2 287.3 7.261 7.95e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Thus,
Salary = 66,333 + 666 x Experience - 8,034 x Gender[T.Male] + 2,086 x Experience:Gender[T.Male]
Now what happens?
- For females, Gender[T.Male]= 0, so
- Salary = 66,333 + 666 x Experience. (Meaning?)
- For males, it is more complicated: Since Gender[T.Male] = 1,
- Salary = 66,333 + 666 x Experience - 8,034 x 1 + 2,086 x 1 x Experience. Simplifying we have,
- Salary = 58,299 + 2,752 x Experience. (Meaning?)
>>Predictions
Suppose you want to estimate a fair salary for a male with 13 years of experience. We do this:
New <- data.frame(Experience=13, Gender="Male")
New
predict(LinearModel.1,New,interval="prediction")
- This gives us
- fit lwr upr
1 94087.71 64075.43 124100
¶
Note 1 : There is an even easier way to get the same results. Just enter Gender=="Male" in the subset box in Linear model, and R gives the regression results for males, only. (Note the double ==.) You can do this as an Exercise. ¶
Note 2: [Caveat! Advanced material] What exactly do we mean by "interaction." Let me make it more clear by comparing two functions (assuming you know some calculus), (i) f(x,y) = ax + by, and (ii) g(x,y) = ax + by + cxy.
In the first case, there is no interaction between x and y, but in the second there is!
Here's why: df/dx = a, so that df = a*dx, i.e., the changes in y do not affect f in this case.
But for the second function, dg/dx = a + cy, so that dg = (a + cy)*dx, i.e., changes in y do affect g!
b.3 Nonlinear relationships and logarithmic data transformations (Will be covered)
- Background material for data transformations from Wikipedia.
- You can think of a logarithm (log) as some mechanism that squeezes a number into a smaller value. For example, 10 becomes 1, 100 becomes 2, 1000 becomes 3, etc.
- Richter scale (6, 7, etc.) is a logarithmic number.
First, an example!
Example : (UN Data) Here is a fascinating example with dataset from the United Nations on a country's GDP and the infant mortality. (You read it from within Rcmdr via "Data > Data in Packages > Read Data From Attached Package > carData > UN". The data file is in native R format, i.e., it is not an Excel file.)
Here is the same file in our usual .csv format: UN.csv
The data is highly nonlinear and a linear fit gives terrible results. But a log transformation of both variables produces a reasonably linear cloud of points through which we fit a line quite accurately.
¶
Example: (Price vs. Demand) Let's consider this data set [Table 4.2 PriceAndDemand.csv] for this example. The scatterplot reveals that there may be a nonlinear relationship between price and quantity. Initially, we fit a line to the data and obtain an R^2 = 0.6236. The graphs obtained for the model reveal that the assumption of errors being normal is not satisfied. When we further do a scatterplot with log x and log y axes, the graph of transformed data appears more linear. A fit using log(Price) and log(Qty) gives the coefficient b = -1.1810 which means that for a 1% increase in price, quantity demanded would reduce by about 1.181%. Here is the output of the results. In this example, we use the Linear Model (not Linear Regression) since we need to enter log(Qty) and log(Price).
¶
Now, a bit of "theory."
Suppose you are not convinced that a linear relationship between price (P) and demand (D) is justifiable; so you decide to use a nonlinear one, e.g., D = exp(a)*P^b where a and b are your coefficients. If you differentiate both sides, we get
dD/dP = exp(a)*b*P^(b-1) = b*exp(a)*P^b*(1/P) = b*D/P.
Rewriting, we have,
dD/D = b*dP/P,
which says that if you increase price P by 1%, demand D will change by b%. (For example, if P = 100, dP = 1, then dP/P = 1%. Now, if b = -2.5, this means that dD/D = -2.5%, so demand will go down by 2.5%.)
Now, taking the logarithms of both sides of D = exp(a)*P^b, we get log(D) = a + b*log(P), which is a nice linear equation, if you write y = log(D) and x = log(P). This means that we can do whatever we were doing as before on the log transformed problem and use the results keeping in mind the meaning of the coefficient b. This is what we will do next. ¶
The interpretation of the estimates of the coefficients will be provided in the next two examples.
>>Predictions
To predict sales for a price of, say, 5 dollars, we enter
newPoint <- data.frame(Price=5)
predict(LinearModel.1,newPoint)
The result is 7.300391 which is the logarithm of the Qty. Converting, we use exp(7.300391) and get
> exp(7.300391)
[1] 1480.879
So, the predicted demand (Qty) is about 1480 units.
¶
Note: Suppose demand D is influenced by price P and another variable, say, average salary S. We then write D = exp(a)(P^b1)(S^b2). Taking logarithms, we get log(D) = a + (b1)log(P) + (b2)log(S) which is now a linear multiple regression model where we need to estimate a, b1 and b2. Earlier results apply.
Top of page
(c) Topic 3: Making models more selective [Chapter 5 in Jank] Multicollinearity, variable selection by stepwise regression
c.1 Multicollinearity
-
- Background material on multicollinearity on Wikipedia.
Is it always a good idea to include as many independent variables as we can in a regression problem? No! Let's see why.
Example: (BIG Trouble!) Consider the dataset [Table5.1Sales-and-Assets.csv] for a problem with sales and assets as independent variables and profit as the dependent variable.
-
If we include both sales and assets in
our problem we find very high p-values for both (0.340 and 0.643) indicating that they are not individually significant, and so they are useless! However, the F-value for the model is very small (0.002), now indicating that the model with these two variables is significant. There is also a high R-squared value (0.63). How could this be?
- There is more to this. When we run the regression with a single variable (Profit vs. Sales, and Profit vs. Assets) we get logical results. Individually, both variables are significant! So, all of this tells us that jointly the two variables do not contribute to our understanding, but individually, they do.
- The reason is that these variables are highly correlated as we see in the correlation matrix.
- Here are the results from Rcmdr.
- How do we cure this problem? By "Variable Selection."
¶
Exercise: (BIG Trouble!) Use this dataset [Butler-x1-x2-Multicollinear.csv] to find a regression equation for Time as dependent variable and Km, Deliveries and Gas (consumed) as independent variables. Is there a high correlation between Km and Gas? What can go wrong with such problems?
-
- Background material on variable selection on Wikipedia.
R has a nice way of dealing with the multicollinearity problem using stepwise regression.
Example: (Stepwise) We use the same dataset [Table5.1Sales-and-Assets.csv] as above. The stepwise procedure is applied after the regression problem is solved by using Models > Stepwise Model Selection... Here is the result.
- We use the Akaike Information Criterion (AIC) and the backward/forward direction.
- Smaller the AIC, the better is the model.
- Start: AIC = 175.64 and
Profit ~ Assets + Sales
- If R removes Assets, we get the smallest AIC value 173.92.
- Any further removal (of Sales) results in a higher AIC, so R stops.
- Thus, we have Profit = -124.85492 + 0.02918 x Sales.
- Note: Everyting is done by R!
¶
Exercise: Consider again the house price dataset [HousePrices-Data.csv] for 124 houses.
- Generate a correlation plot using corrplot for all the numerical variables.
- Run a regression with Price as the dependent variable and everything else (except SubDiv) as independent variable.
- Next, use Models > Stepwise Model Selection... and reduce the model with Akaike Information Criterion (AIC) and the backward/forward direction.
- How many independent variables do you have left and what is the AIC? (Answer: We have 5 variables left as, Price ~ Bathrooms + Bedrooms + Distance + LotSize +
SqrFt, and AIC is 736.41.)
Top of page
(d) Topic 4: Data modelling - Fine-tuning your model [Chapter 6 in Jank: Sec. 6.1 and Sec. 6.2.2] Regression with trend and seasonality, nonparametric regression
d.1 Nonparametric regression (Not covered in Fall 2017 T711)
This topic will probably be covered online (post-residence), but here are some details about it.
Up to this point we always assumed a parametric form for our models. In linear models, we had, e.g., D = a + bP for price/demand relationship. In nonlinear, log-transformed models, we had D = exp(a)P^b which was transformed to log(D) = a + blog(P).
What if we can't make any assumptions about our models? If so, we just need to do some sophisticated curve-fitting which is the idea behind "Nonparametric Regression." Here's an example.
Example: (Nonparametric) Let's consider again this data set [Table 4.2 PriceAndDemand.csv] for this example. We now use Statistics > Fit Models > Linear Model. Here, we use the B-spline option and for dependent variable we enter Qty. For independent variable we now have bs(Price, df = 5) which works well for most problems. The results are found as,
> summary(LinearModel.1)
Call:
lm(formula = Qty ~ bs(Price, df = 5), data = Dataset)
Residuals:
Min 1Q Median 3Q Max
-238.67 -131.92 -24.93 118.85 361.72
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2724.0 133.9 20.349 < 2e-16 ***
bs(Price, df = 5)1 -773.5 269.4 -2.872 0.00626 **
bs(Price, df = 5)2 -1112.9 182.3 -6.106 2.36e-07 ***
bs(Price, df = 5)3 -1511.0 194.5 -7.768 8.71e-10 ***
bs(Price, df = 5)4 -1363.1 189.0 -7.212 5.60e-09 ***
bs(Price, df = 5)5 -1525.4 203.9 -7.483 2.25e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 166.2 on 44 degrees of freedom
Multiple R-squared: 0.7926, Adjusted R-squared: 0.7691
F-statistic: 33.64 on 5 and 44 DF, p-value: 5.63e-14
Note the high R^2. We can also do predictions as before, and obtain,
> newPoint <- data.frame(Price=5)
> predict(LinearModel.1,newPoint)
1
1424.84
This predicted value is close to the result we found in the log-transformation case.
¶
Note: Suppose demand D is influenced by price P and another variable, say, average salary S. Even if we can't make any assumptions about the model, we can still use the nonparametric approach. In this case, we would enter
lm(formula = Qty ~ bs(P, df = 5) + bs(S, df = 5), data = Dataset)
This would solve the problem with two variables. Earlier results apply.
d.2 Term Project Information
- Once we understand nonlinear regression, we are ready for the Term Project!
- I will give you a huge dataset of financial indicators and ask you to "predict" the stock price of a company.
- This dataset has a large number of highly correlated variables (discovered via corrplot).
- You will then do,
- stepwise regression
- nonlinear regression
- We will then consider the UN data of infant mortality and will
- do nonlinear regression/prediction and finally,
- prepare a report.
Top of page
 vs.
vs. 






